정렬 알고리즘 - 합병 정렬
August 14, 2022
JavaScript 알고리즘 & 자료구조 마스터 클래스 강의를 듣고 작성하는 강의노트
합병 정렬 (Merge Sort)
- 배열의 길이가 0 또는 1이라면 이미 정렬되어 있다는 점을 활용한다.
- 정렬되어 있지 않다면, 배열을 더 작은 배열로 나누는 방식으로 분할정복 알고리즘의 하나이다.
- 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬 후, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
- 합병 정렬은 분할, 정복, 결합으로 이루어진다.
- 분할(Divide): 입력 배열을 요소 하나씩 분리될 때까지 2분할 한다.
- 정복(Conquer): 분할한 부분 배열을 정렬한다.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
정렬되는 과정
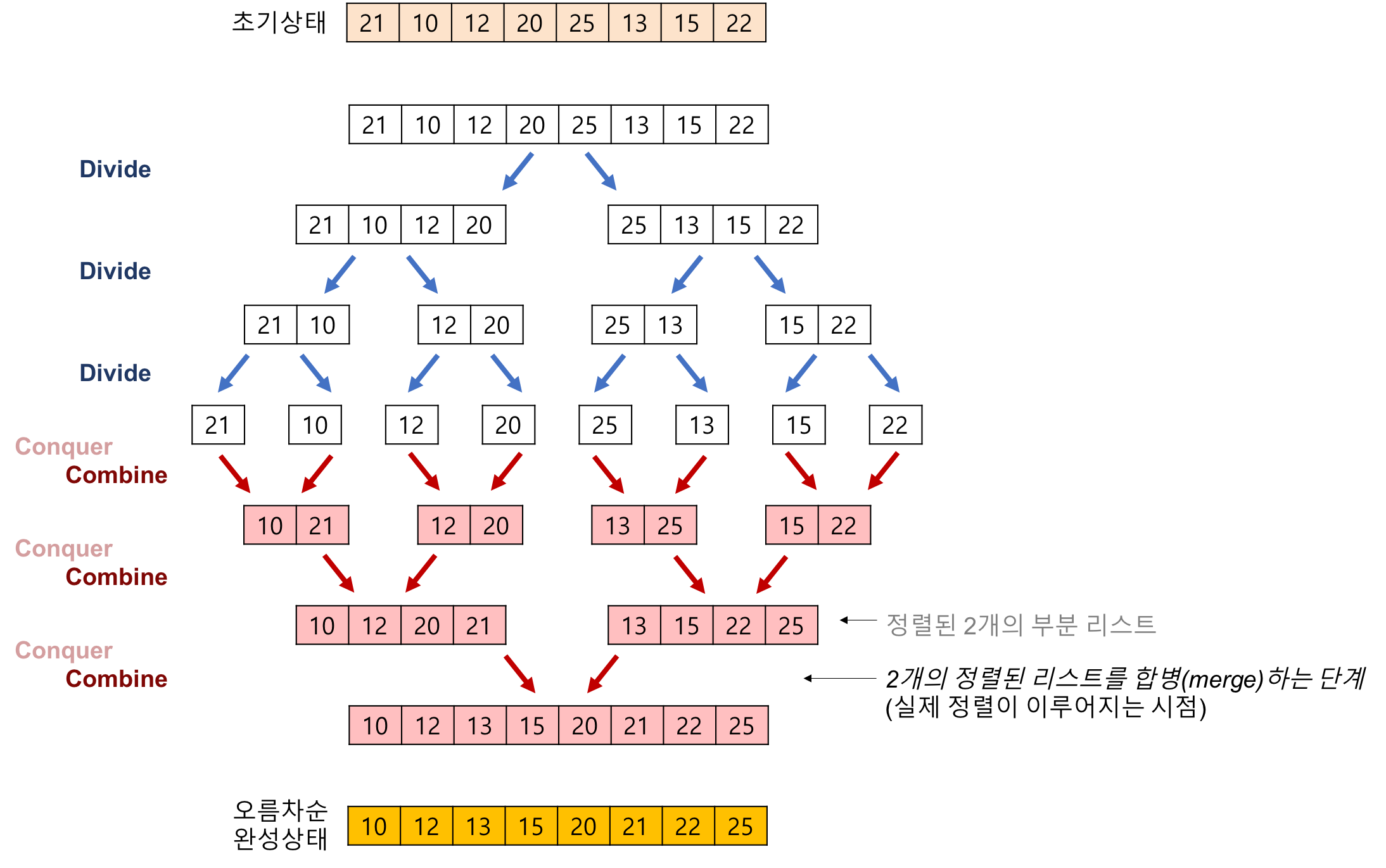
사진 출처: https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
배열의 합병 구현
두 배열을 인자로 받는 함수를 정의한다.
function merge(arr1, arr2) {
// 합병 결과를 저장할 빈 배열
let results = [];
let i = 0; // arr1의 포인터
let j = 0; // arr2의 포인터
/* arr의 포인터와 arr2의 포인터가 각 배열의 길이보다 짧을 때 */
while (i < arr1.length && j < arr2.length) {
// 각 포인터가 가리키는 요소끼리 비교
if (arr2[j] > arr1[i]) {
results.push(arr1[i]);
i++;
} else {
results.push(arr2[j]);
j++;
}
}
/* arr1에 비교하지 못한 남은 요소가 있을 경우 */
while (i < arr1.length) {
results.push(arr1[i]);
i++;
}
/* arr2에 비교하지 못한 남은 요소가 있을 경우 */
while (j < arr2.length) {
results.push(arr2[j]);
j++;
}
return results;
}수행 과정
배열 요소 위 언더바(_)는 포인터를 표현
merge([1, 10], [2, 14, 99]);1회전
_ _
[1, 10], [2, 14, 99]
1 과 2를 비교 후 저장 더 작은 값을 저장
결과: [1]
2회전
__ _
[1, 10], [2, 14, 99]
10 과 2를 비교 후 저장 더 작은 값을 저장
결과: [1, 2]
3회전
__ __
[1, 10], [2, 14, 99]
10 과 14를 비교 후 저장 더 작은 값을 저장
결과: [1, 2, 10]
4회전
__
[1, 10], [2, 14, 99]
첫 번째 배열을 모두 순환했으므로 남은 두번째 배열 순환
결과: [1, 2, 10, 14]
5회전
__
[1, 10], [2, 14, 99]
50 과 99를 비교 후 저장 더 작은 값을 저장
결과: [1, 2, 10, 14, 99]
합병 정렬 작성
위에서 구현한 merge 함수와 재귀를 활용하여 합병정렬을 구현한다.
- 인자로 받은 배열의 중간지점으로부터 left, right으로 쪼갠다.
- 길이가 1보다 같거나 작을 때까지 재귀적으로 수행한다.
- 위에서 구현한 배열의 merge 함수를 수행하여 정렬한다.
function mergeSort(arr) {
if (arr.length <= 1) return arr;
let middle = Math.floor(arr.length / 2);
let left = mergeSort(arr.slice(0, middle));
let right = mergeSort(arr.slice(middle));
return merge(left, right);
}
mergeSort([10, 24, 76, 73, 72, 1, 9]);
// output: [1, 9, 10, 24, 72, 73, 76]빅오(Big O)
시간복잡도
| Best Complexity | Average Complexity | Worst Complexity |
|---|---|---|
| O(n log n) | O(n log n) | O(n log n) |
공간 복잡도
| Space Complexity |
|---|
| O(n) |