빅오(Big O)

August 6, 2022

JavaScript 알고리즘 & 자료구조 마스터 클래스 강의를 듣고 작성하는 강의노트

빅오(Big O) 개념

알고리즘의 해결법은 수십가지가 있을 것이다. 그 중 가장 좋은 해결법이 무엇인지 어떻게 평가할까? 두가지의 해결법이 있다고 가정해볼 때, 두 해결법은 모두 정답이지만 다르다. 단순히, For loop를 While loop 로 바꾸는 정도를 벗어나 ^문제를 접근하는 방식^ 자체가 다르다.

이때 빅오(Big O)를 통해 어떤 접근법이 더 좋은지, 여러 코드를 비교하여 성능을 평가할 수 있다.

코드의 성능을 이야기할 때 정확한 전문용어를 사용하는 것이 중요하다.
본인의 풀이와 다른 풀이들을 비교하고 성능이 어떤지 이해하는 데 유용하다.
코드를 디버그할 때 코드의 속도를 느리게 만드는 문제점을 찾고 이해하는 데 도움이 된다.
코드가 실행될 때 걸리는 시간을 초로 측정하는 것보다, 컴퓨터가 처리해야하는 연산 갯수를 세는 것이 성능 비교에 용이하다. (어떤 컴퓨터를 사용하든 갯수는 변하지 않기 때문에.)

더 나은 코드의 기준

속도
메모리 샤용량
가독성

연산 갯수에 따른 코드 비교

1부터 인자로 전달받은 수까지의 합을 구하는 함수로, 두 개의 예시를 들어보자.

case 1

function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

위 코드는 어떤 수가 인자로 들어와도 *, +, / 연산이 각각 한번씩 총 3번 실행된다.

case 2
for loop 를 사용한 코드다.

function add(n) {
  let total = 0;
  for (let i = 0; i <= n; i++) {
    total += i;
  }
  return total;
}

해당 코드는 연산을 몇번 실행할까? 인자로 전달받는 수(n)에 따라서

let total = 0 의 = 연산 한번
for loop의 i = 0 연산 한번
for loop의 i <= n 연산 n번
for loop의 i++ 연산 n번
total += i 의 + 연산 n번
total += i의 = 연산 n번

총 5n+2 번 일어난다. 즉, case 1 의 속도가 더 빠른 것을 알 수 있다.

빅오(Big O) 란?

입력된 내용이 늘어날 수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식으로 알고리즘의 시간 복잡도를 나타내는 표기법이며, O(f(n))으로 나타낸다.

쉽게 말해 어떤 함수의 입력 값이 늘어나는 것과 실행 시간이 변하는 관계, 입력의 크기와 실행시간의 관계를 말한다.

빅오(Big O)의 정의

컴퓨터가 해야하는 간단한 연산의 수 n이 증가함에 따라 f(n)의 상수보다 적다면 그 알고리즘은 Big O 표기법으로 O(f(n)) 이라고 표현한다.

f(n) = n - n이 커질수록 실행 시간도 늘어나는 선형관계 = O(n)
f(n) = n^2 - n이 커질수록 실행시간은 n의 제곱이 되는 이차함수 관계 = O(n²)
f(n) = 1 - n이 커져도 실행시간에 영향을 받지 않는 상수 관계, 이를 단순하게 1이라고 표현 = O(1)
입력 값과 실행시간이 완전히 다른 관계

따라서 위에서 들었던 예시 케이스 중 case 1 은 상수이므로 O(1) 라고 표현하고, case 2 는 5n 이든 10n 이든 상관하지 않고 O(n) 아라고 표현할 수 있다.

다음 예시 또한 2n 으로 볼 수 있지만 2n 이든 5n이든 상관하지 않기 때문에 n, 즉 O(n)으로 표현한다.

function countUpNDown(n) {
  console.log('up');
  for (let i = 0; i < n; i++) {
    // O(n)
    console.log(i);
  }
  console.log('down');
  for (let j = n - 1; j >= 0; j++) {
    // O(n)
    console.log(j);
  }
}

그렇다면 다음 예시는 어떨까?

해당 코드는 단순히 O(n)으로 볼 수 없다. 코드가 중첩되어있기 때문에 O(n²)으로 표현한다.

function print(n) {
  for (let i = 0; i < n; i++) {
    // O(n)
    for (let i = 0; i < n; i++) {
      // O(n)
      console.log(i);
    }
  }
}

빅오(Big O) 표기법 단순화

1. 상수는 중요하지 않다.

상수 값이 다르다고 해도 그래프로 나타냈을 때는 차이가 없기 때문에 중요하지 않다.

O(2n) = O(n)
O(500) = O(1)
O(13n²) = O(n²)

각 표기법에 따른 속도: O(1) > O(n) > O(n²)

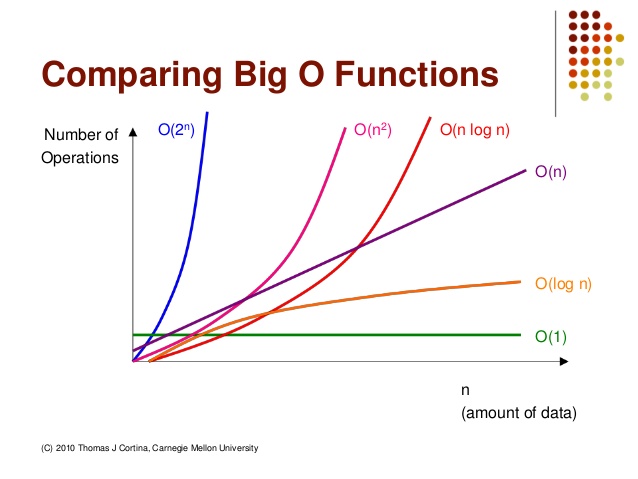
^{https://velog.io/@kyunghwan1207/알고리즘-시간복잡도Time-Complexity와-Big-O표기법Big-O-Notation}

2. 작은 연산은 중요하지 않다.

O(n + 10) = O(n)
O(1000n + 50) = O(n)
O(n² + 5n + 8) = O(n²)

알아야할 것

산수는 상수다. 덧셈, 뺄셈, 곱셈, 나눗셈을 포함한다.
변수 배정 또한 상수다.
인덱스를 통해 배열 엘리먼트에 접근하는 것은 배열에서 몇번째 아이템을 찾던지 모두 똑같은 시간이 걸리므로 실행 시간은 상수다. 객체 의 키를 통한 접근 또한 상수다.
loop가 있다면 복잡도가 '루프의 길이 x 루프 안에 있는 연산들'이 된다.
0 에서 n 까지 간다면 n이 커질수록 루프가 반복되는 횟수가 늘어난다.
중첩 루프가 있다면 n의 제곱 실행 시간이 될 수 있다.

공간 복잡도

입력이 커질수록 알고리즘이 얼마나 많은 공간(사용되는 메모리)을 차지하는지 표현

공간 복잡도 규칙

boolean, number, undefined, null은 자바스크립트에서 모두 불변 공간이다.
- 입력의 크기와 상관없이 숫자가 1이든 1000이든 모두 불변 공간 O(1)
문자열은 O(n)공간이 필요하다.
reference 타입, 배열, 객체도 O(n)

로그 함수

간단하게 말하면, 로그함수는 지수 함수의 역함이다.

log₂(8) = 3

thisyujeong.dev